二叉查找树
本文共 5960 字,大约阅读时间需要 19 分钟。
来源:
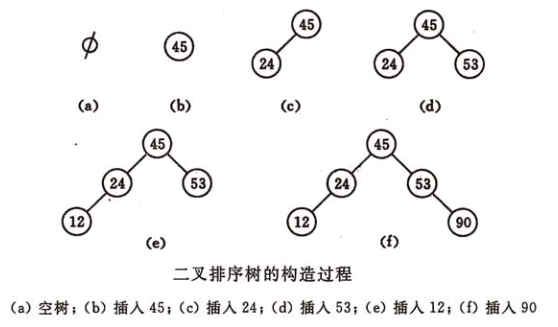
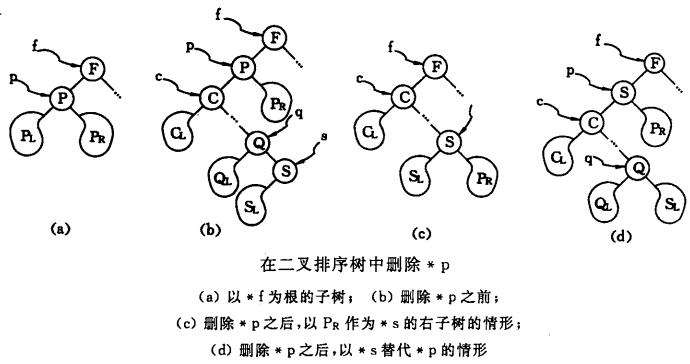
/* ****************************************************************************** /* <PRE> /* 版权所有 : - /* 模块名 : 查找 /* 文件名 : bitreeSearch.cpp /* 功能描述 : 二叉排序树 /* 作者 : <xxx> /* 版本 : 1.0 /* ----------------------------------------------------------------------------- /* 备注 : - /* ----------------------------------------------------------------------------- /* 修改记录 : /* 日 期 版本 修改人 修改内容 /* 2011/01/01 1.0 <xxx> 创建 /* </PRE> ****************************************************************************** */ #include < stdio.h > #include < stdlib.h > /* ***************************************************************************** /* 数据类型和常量定义 /***************************************************************************** */ #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define OVERFLOW -2 typedef int Status; /* 函数结果状态码 */ typedef int KeyType; /* 整型关键字 */ /* 数值型关键字的比较 */ #define EQ(a, b) ((a) == (b)) #define LT(a, b) ((a) < (b)) /* ***************************************************************************** /* 数据结构定义 /***************************************************************************** */ /* 数据元素类型定义 */ typedef struct { KeyType key; // 关键字域 }ElemType; /* 二叉树的链式存储结构 */ typedef struct BiTNode { ElemType data; struct BiTNode * lchild, * rchild; } BiTNode, * BiTree; /* ***************************************************************************** /* 函数原型声明 /***************************************************************************** */ Status SearchBST(BiTree T, KeyType key, BiTree f, BiTree & p); Status InsertBST(BiTree & T, ElemType e); Status DeleteBST(BiTree & T, KeyType key); Status Delete (BiTree & p); Status Visit(ElemType e); Status InOrderTraverse(BiTree & T, Status ( * Visit)(ElemType)); /* ****************************************************************************** /* <FUNC> /* 函数名 : SearchBST /* 功能 : 二叉排序树的查找方法 /* 参数 : - /* 返回值 : - /* 备注 : 在根指针T所指二叉排序树中递归地查找其关键字等于key的数据元素, 若查找 /* 成功, 则指针p指向该数据元素结点, 并返回TRUE, 否则指针p指向查找路径上 /* 访问的最后一个结点并返回FALSE, 指针f指向T的双亲, 其初始调用值为NULL /* 作者 : <xxx> /* </FUNC> ****************************************************************************** */ Status SearchBST(BiTree T, KeyType key, BiTree f, BiTree & p) { if ( ! T) {p = f; return FALSE;} // 查找不成功 else if EQ(key, T -> data.key) {p = T; return TRUE;} // 查找成功 else if LT(key, T -> data.key) return SearchBST(T -> lchild, key, T, p); // 在左子树中查找 else return SearchBST(T -> rchild, key, T, p); // 在右子树中查找 } /* ****************************************************************************** /* <FUNC> /* 函数名 : InsertBST /* 功能 : 插入元素到二叉排序树中 /* 参数 : - /* 返回值 : - /* 备注 : 当二叉排序树T中不存在关键字等于e.key的数据元素时, 插入e并返回TRUE, /* 否则返回FALSE /* 作者 : <xxx> /* </FUNC> ****************************************************************************** */ Status InsertBST(BiTree & T, ElemType e) { BiTree s; BiTree p; if ( ! SearchBST(T, e.key, NULL, p)) { // 查找不成功 s = (BiTree)malloc( sizeof (BiTNode)); s -> data = e; s -> lchild = s -> rchild = NULL; if ( ! p) T = s; // 被插结点*s为新的根结点 else if LT(e.key, p -> data.key) p -> lchild = s; // 被插结点*s为左孩子 else p -> rchild = s; // 被插结点*s为右孩子 return TRUE; } else return FALSE; // 树中已有关键字相同的结点, 不再插入 } /* ****************************************************************************** /* <FUNC> /* 函数名 : DeleteBST /* 功能 : 从二叉排序树中删除一个结点 /* 参数 : - /* 返回值 : - /* 备注 : 若二叉排序树T中存在关键字等于key的数据元素时, 则删除该数据元素结点, /* 并返回TRUE; 否则返回FALSE /* 作者 : <xxx> /* </FUNC> ****************************************************************************** */ Status DeleteBST(BiTree & T, KeyType key) { if ( ! T) return FALSE; // 不存在关键字等于key的数据元素 else { if (EQ(key, T -> data.key)) { return Delete(T); } // 找到关键字等于key的数据元素 else if (LT(key, T -> data.key)) return DeleteBST(T -> lchild, key); else return DeleteBST(T -> rchild, key); } } /* ****************************************************************************** /* <FUNC> /* 函数名 : Delete /* 功能 : 删除一个结点的过程 /* 参数 : - /* 返回值 : - /* 备注 : 从二叉排序树中删除结点p, 并重接它的左或右子树 /* 作者 : <xxx> /* </FUNC> ****************************************************************************** */ Status Delete (BiTree & p) { BiTree q; BiTree s; if ( ! p -> rchild) { // 右子树空则只需重接它的左子树 q = p; p = p -> lchild; free(q); } else if ( ! p -> lchild) { // 只需重接它的右子树 q = p; p = p -> rchild; free(q); } else // 左右子树均不空 { q = p; s = p -> lchild; while (s -> rchild) {q = s; s = s -> rchild; } // 转左, 然后向右到尽头 p -> data = s -> data; // s指向被删除结点的前驱 if (q != p) q -> rchild = s -> lchild; // 重接*q的右子树 else q -> lchild = s -> lchild; // 重接*q的左子树 delete s; } return TRUE; } /* ****************************************************************************** /* <FUNC> /* 函数名 : Visit /* 功能 : 打印节点数据 /* 参数 : - /* 返回值 : - /* 备注 : - /* 作者 : <xxx> /* </FUNC> ****************************************************************************** */ Status Visit(ElemType e) { printf( " %d " , e.key); return OK; } /* ****************************************************************************** /* <FUNC> /* 函数名 : InOrderTraverse /* 功能 : 中序遍历二叉树 /* 参数 : - /* 返回值 : - /* 备注 : - /* 作者 : <xxx> /* </FUNC> ****************************************************************************** */ Status InOrderTraverse(BiTree & T, Status ( * Visit)(ElemType)) { if (T){ if (InOrderTraverse(T -> lchild, Visit)) if (Visit(T -> data)) if (InOrderTraverse(T -> rchild, Visit)) return OK; return ERROR; } else return OK; } /* ****************************************************************************** /* <FUNC> /* 函数名 : main /* 功能 : 测试函数 /* 参数 : - /* 返回值 : - /* 备注 : - /* 作者 : <xxx> /* </FUNC> ****************************************************************************** */ void main() { BiTree T = NULL; ElemType e; int i, j; // 插入元素 for (i = 1 ; i <= 5 ; i ++ ) { e.key = i; InsertBST(T, e); } for (i = - 5 ; i <= - 3 ; i ++ ) { e.key = i; InsertBST(T, e); } printf( " elems inserted: " ); InOrderTraverse(T, Visit); // 删除元素 for (j = - 5 ; j <= 4 ; j ++ ) { DeleteBST(T, j); } printf( " \nremaining after delete: " ); InOrderTraverse(T, Visit); }
转载地址:http://xvuoo.baihongyu.com/
你可能感兴趣的文章
中间件详解,Django复习
查看>>
微信小程序 md5加密
查看>>
python gui之tkinter事件处理
查看>>
Android Studio 1.1.0 切换主题和绑定 代码提示 快捷键
查看>>
读书笔记 UltraGrid(8)
查看>>
Spring Boot文档维护:集成Swagger2
查看>>
SharePoint 2010 部署架构
查看>>
BZOJ[3992][SDOI2015]序列统计 生成函数+NTT
查看>>
GUI自绘_其中左边树状菜单控件风格灵感来源于城市博物馆的壁灯效果。
查看>>
SSH 相关基础
查看>>
浅谈git和svn的区别
查看>>
JMETER 生成测试报告
查看>>
ScrollView中嵌套ListView
查看>>
XML再深入
查看>>
顺序表基础操作--练习
查看>>
Spring Cloud底层原理
查看>>
SSM前言——相关设计模式
查看>>
小清丽微距花卉拍摄示范
查看>>
GetSysColor()函数可以得到系统的颜色
查看>>
项目积累demo-01
查看>>